
 |
|
||||||||
13. Discounting with the Euler number exponential function in economic models of vessel or the property complex of marine company’s real assets
The material of the given section material contains the analysis of approximation accuracy of the discounting factor determined by arithmetic summation (1+i) and estimations of present value for investing into development of the ocean wealth, by the discount financial functions, and it also contains the analysis of methodological advantages of formulas of the discount financial functions based on application of exponential functions of the Euler number e = 2.71828283..., that, is the bases of the natural logarithm.
It is considered that when investing in industrial activity for the ocean resources development is more effectively and accordingly more risky economically than investing in the financial deposit in respect of which the discounting by the exponential functions of the factor calculated by the arithmetic summation (1+i) is accepted.
In applied tasks to determine the total risk depending on its separate components the expert methods of the hypothec–investment group in particular, the following methods of the discounting rate calculation are usually recommended: the cumulative estimation, the models of capital assets estimation, the models of the average weighted cost of the capital etc., and also methods of the arbitration pricing or the extraction which though are not formally based on risks summation, but are alternative ways of calculation of the index of the discounting rate which is total of the risks.
At the same time for present values estimation is required not only correct calculation of the total risk depending on separate components, but also the development of the adequate discounting method when the properties of summable risk components which correspond to actions in sequence of innovative investing in real assets of the marine companies’ complexes of the assets are taken into account.
The analysis of applicability of discounting by the Euler number exponential function and advantages of this method, for present value estimation of the marine company’s real assets with the account of the formal–logic properties of risks probablistic concept.
The financial functions based on discounting by exponential of the factor calculated by arithmetic summation (1+i) based on monetary rules of interest accruing on the financial deposit determination (or the mortgage) are the approximate ways of present value and financial indexes determination and are rather exact at the limited risks i correlated, on the other hand, with investments efficiency.
The arithmetic summation of the discounting rate to a one in case of factor of discounting (1+i) determination is based on the general assumption that the risk is the one–factorial index corresponding to the discounting rate i, and it is rather true if financial investment strategy means a single action – the financial deposit (or the mortgage).
If innovative strategy in the marine industrial activity on investing financial assets in real assets is an actions sequence, the general risk insufficiently precisely corresponds to the estimation by the one–factorial index and each action in strategic sequence influences strategy total risk value.
It should be reasonable to research the methodological correctness of risks summation from the mathematical point and discounting by the factor (1+i).
The commercial risk in estimation can be correlated with the discounting index i or 1-(1-i). When determining the total risk as a probablistic characteristic of the sequence of casual events it is necessary to take into account that the probability of events sequence corresponds to the product of probability of each event by the probability of previous events or to the multiplication of events probabilities in sequence.
| i=1-(1-i)=1-(1-i1)×(1-i2)×...×(1-in)=1-(1-i1- i2-...- in+ i1×i2+...+i1×in+i1×in-...- i1×i2×...×in | (13.1) |
i=1-(1-i)=1-(1-i1-i2-...-in,) |
(13.2) |
|
(13.3) |
or i=1-(1-i/n)n.
The limiting value of commercial risk at its division into the great number of the components ![]() is equal:
is equal:
As, on the other hand, the total commercial risk corresponds (is approximately equal) to the discounting rate, then i ≈1-1/ei, or, after derivation, the factor of discounting based on the exponential functions of the Euler number application is determined as ei≈1+i.
The discounting rate as an indicator of the commercial risks total methodologically more precisely corresponds to the factor in exponential function of the Euler number ei or exp(i), than the member in the sum of discounting factor (1+i), as the factor of discounting as exponential function of the Euler number ei grows out in case of summation of risks in frameworks of the complete–probablistic estimation scheme with multifactorial characteristics of the general risk (13.3) as a form of use of the discounting rate of innovative strategy commercial risk unlike the factor of the discounting calculated by arithmetic summation (1+i) which is more suitable for determining the present values with one–factorial risks of the financial investment in the monetary deposit (or the loan).
With rather small total investment risks i≤0,15÷0,20 of discounting factor the value of the discounting factor determined on the basis of the Euler number exponential function ei and on the basis of arithmetic summation (1+i) are approximately equal and in applied tasks lead to a rather close present value. In case of increase in investment risks i there is a difference of discounting factors ei and (1+i), tab. 13.1, fig. 13 .
Table 13.1
The dependences of the factors determined by the arithmetic summation (1+i) and the Euler number exponential function ei on discounting rate i
i |
5 % |
10 % |
15% |
20% |
25% |
30% |
35% |
40% |
45% |
50% |
(1+i) |
105 % |
110 % |
115% |
120% |
125% |
130% |
135% |
140% |
145% |
150% |
ei |
105 % |
111 % |
116% |
122% |
128% |
135% |
142% |
149% |
157% |
165% |
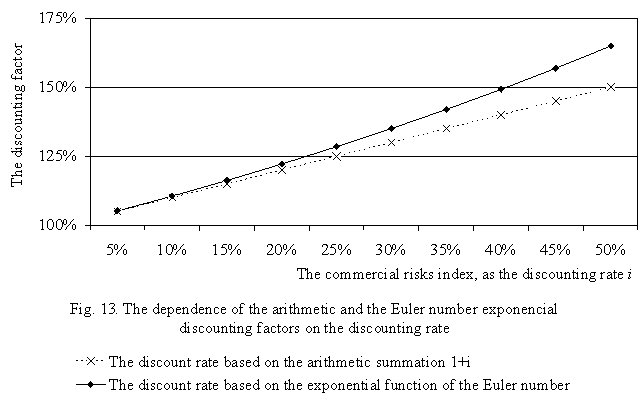
It should be noted that the discounting factor as exponential function of the Euler number ![]() is the form of the remainder account (13.3) that is a difference
is the form of the remainder account (13.3) that is a difference ![]() between the total risk values determined by the complete–probablistic scheme (13.1) and by the cumulative estimation (13.2).
between the total risk values determined by the complete–probablistic scheme (13.1) and by the cumulative estimation (13.2).
The factor of discounting as an exponential function of the Euler number ![]() corresponds to present value estimation of innovative strategy with the multifactorial risks of consecutive actions if the total risk is rather great, and the strategy is as effective as in case of investing in real assets of the marine companies’ complexes of the assets using which the investor gets an access to marine wealth.
corresponds to present value estimation of innovative strategy with the multifactorial risks of consecutive actions if the total risk is rather great, and the strategy is as effective as in case of investing in real assets of the marine companies’ complexes of the assets using which the investor gets an access to marine wealth.
Though with smaller risks and rates, as in case of financial investing in the monetary deposit, the application of the factor of discounting as the exponential function of the Euler number ![]() is quite reasonable, as the factor of discounting determined by summation (1+i) with small risks correlated with index of the discounting rate
is quite reasonable, as the factor of discounting determined by summation (1+i) with small risks correlated with index of the discounting rate ![]() , is rather close numerical approximation of discounting factor as the exponential function of the Euler number
, is rather close numerical approximation of discounting factor as the exponential function of the Euler number ![]() .
.
Perhaps, the choice of discounting method from the two considered options with small risks depends basically on the expert’s ability to determine exponential function value and on formal–logic understanding properties of risks probablistic concept that provides the confidence of choice of present values of real assets as a part of the marine company’s property complex.
It should be added that discounting by the Euler number exponential function ![]() is also determined on the basis of present value potential equation integration (Chapter 4, the formula 4.1) when developing the form of the statistical regression for generalization of the marketing researches data concerning value of the assets, which pricing quite precisely can be laid in the property complex evaluation scheme with value of the asset proportional to the company complex of assets total value, for example of the marine commercial vessels and such assets, which value essentially depends on years.
is also determined on the basis of present value potential equation integration (Chapter 4, the formula 4.1) when developing the form of the statistical regression for generalization of the marketing researches data concerning value of the assets, which pricing quite precisely can be laid in the property complex evaluation scheme with value of the asset proportional to the company complex of assets total value, for example of the marine commercial vessels and such assets, which value essentially depends on years.
With the account the recommendation concerning preference of discounting by the Euler number exponential function the method of the discounted cash flow capitalization for vessel value estimation (or the isolated asset) as a part of the marine company’s property complex becomes:
– For the continuously accumulating sum of the discounted cash flow and with the set duration of the forecasting period T it is determined as:
(13.4) |
|
(13.5) |
Tn+1-Tn=ln(NOIn+1/NOIn)/i. |
(13.6) |
Table 13.2
Six standard discount financial functions corresponding to the discounting factors determined by summation 1+i and by the Euler number exponential function ei or exp(i)
| The factor of discounting defined by summation 1+i | The discounting by the Euler number exponential function ei or exp(i) |
If the rate i is defined based on methods of hypotec–investment group (cumulative estimation, etc.) it is recommended to correct the value of the discounting rate by operation i≈ei-1 for use in case of discounting by the factor (1+i) |
If the rate i is determined according to market research by transformation of data on the basis of discounting by factor (1+i) it is recommended to correct the value of the rate by operation i≈ln(1+i) for use in case of discounting by the Euler number exponential function ei |
1. The future value FV (complex percent), that is the present single investment, t – present time (or a number of the periods of interest accrual) |
|
FV=(1+i)t |
FV=i×t |
2. The future value of annuity FVA (the future at the end of the period to Ò value of single cash flow of the uniform periodicity) |
|
3. The factor of fund of compensation PMT/FVA or |
|
4. The present value PV of unit (discounting) that is present value of future single investment after time t |
|
PV=1/(1+i)t=(1+i)-t |
PV=1/ei×t=e-i×t |
5. The present value of single annuity PVA (the single cash flow uniform of periodicity to Ò) |
|
6. The payment for unit amortization PMT/PVA (repayment of the single loan by equal payments uniform of periodicity to Ò) |
|
Test questions
1.Discounting rate, the discounting factor.
2. Arithmetic summation of risks for determination of the discounting rate by the formula of cumulative estimation.
3. Summation with the account probabilistic characteristic of each risk with the multiplication by the reminder after subtraction of other risks (the formula derivation).
4. Factor of discounting by the Euler number exponential function.
5. Recommendations of discounting by the Euler number exponential function.
6. Formal–logic sense of commercial risk index.
7. Method of cash flow capitalization in case of use of discounting by the Euler number exponential function for the interval form (the formula at the set time interval of discounting to reversion).
8. Form of cash flow capitalization in case of using of the discounting by the Euler number exponential function for intervals of cash flow stability.
9. Definition of investment stages duration with the account continuity of a cash flow by the transformation based on discounting by the Euler number exponential function.
10. Discount financial functions when using arithmetic discounting and the Euler number exponential function (the formula derivation): the future value, the future value of annuity, the factor of fund of compensation, the present value of a unit (discounting), the present value of single annuity, the payment for unit amortization.
11. Factor of discounting determined by summation, based on operation of interest accrual for the mortgage or the deposit.
12. Substantiation of the form of the discounting by the Euler number exponential function factor depending on summation rules of probablistic risks independent components.
 |
 |
|||||